Dans ce billet de blog, je vais tenter de trouver une approximation pour la série postée dans la partie 2. Dans la partie #2, nous avions le tableau :
Tableau 2. Le tableau affiche les X nombre d’investissements qui accumulent de la valeur sur une durée infinie J période. Dans notre modèle, nous avions X = J par conséquent, fixer J à l’infini est une surapproximation évidente. La forme produite par les cellules est rectangulaire (J x X) alors que, comme dans le vrai modèle, elle est triangulaire ~ 1/2 (J x X).
Modifions légèrement les définitions et transformons le tableau rectangulaire en carré. De plus, modifions également la définition de chaque variable de sorte que J = # de périodes qui génèrent un retour sur investissement et X = #investissements + 1. Par exemple, si nous avons 3 investissements pendant 4 périodes, alors nous avons J = X où (J, X) est un tableau (4,4) :
| ROI basé sur la période dans laquelle nous avons investi (1/r) | Somme partielle de chaque investissement | ||||
| Retour sur investissement de la période 1 | Retour sur investissement de la période 2 | ROI de la période 3 | Retour sur investissement de la période 4 | UN1[1-rn]/[1-r] | |
| Investissement #1 | 1/2 $ | 1/4 $ | 1/8 $ | 1/16 $ | ½[(1-1/2)4]/(1-1/2) |
| Investissement #2 | 1/3 $ | 1/9 $ | 1/27 $ | 1/81 $ | 1/3[1-(1/3)4]/(1-1/3) |
| Investissement #3 | 1/4 $ | 1/16 $ | 1/64 $ | 1 $/256 | 1/4[1-(1/3)4]/(1-1/4) |
Nous pouvons donc généraliser la somme de chaque investissement pour tous les retours sur investissement dans les solutions de la colonne de droite comme :
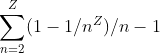
Il ne m’est pas clair comment disséquer mathématiquement cette série. Une tentative consiste à le représenter comme un sous-approximé sous forme intégrale :

En utilisant notre exemple de cas de Z = 4, cela se factorise bien par fractions partielles pour :

Où nous pouvons évaluer chaque individu en nous donnant la forme indéfinie de :

Nous choisissons d’utiliser un Z = 4 car nous avons 3 investissements pour quatre périodes d’intérêt. Nous devons donc calculer cela à travers [4,2]. En développant cela, nous avons:

L’évaluation ci-dessus ne fonctionne que pour Z = 4. Si nous avions plus de périodes de retour sur investissement, nous pourrions également avoir plus d’investissements et donc plus de termes à intégrer. On peut donc essayer de généraliser (#4).
Nous voulons pouvoir écrire le type intégral ci-dessus d’une manière qui puisse être évaluée même lorsqu’il y a 49 investissements sur 50 périodes de retour sur investissement. Cela n’aurait aucun sens d’écrire à la main les 49 polynômes et 1 logarithme pour les bornes inférieure et supérieure. On peut donc essayer de généraliser le modèle pour [2,Z] comme:

Alors

Réflexions finales : Les deux dernières équations sont remarquablement similaires à la somme partielle d’une série de puissances. Aussi intéressant que cela puisse être, il n’est pas évident de résoudre ce problème davantage. J’ai essayé d’utiliser, mais pas même l’intuition de Wolfram alpha sur la façon de résoudre ne serait-ce qu’une des séries. Même si j’ai eu le moment « aha », c’est toujours un pas en arrière. L’approximation faite via notre intégrale (Eq 2) a produit une somme qui s’évalue à environ 0,85 $ (Eq 5) alors que la somme réelle devrait être de 1,76 $. Trouver une forme fermée de (Eq 1) directement au lieu d’utiliser une approximation pourrait en fait être plus rapide que tout essayer de trouver d’autres approximations. Si quelqu’un de meilleur en mathématiques sait comment résoudre ce problème, n’hésitez pas à laisser la solution dans la section des commentaires. J’apprécierais beaucoup. Sinon, j’apprécie que vous lisiez jusqu’ici un article aussi technique.
Merci,
Ben


